Transport optimal : Quelles applications concrètes et financières pour ce vieux sujet ?

 

Le mathématicien Cédric Villani parle « d’un coup de neuf pour un très vieux problème » quand il évoque le transport optimal, en effet, cette théorie a traversé les siècles et ceci par le caractère très concret de ses applications mais également par la richesse des travaux apportés.

Ce sont des notions qui sont très intuitives : par exemple les diagrammes de Voronoï[1], qui correspondent entre autres choses à des formes prises par des taches sur le pelage de certains animaux (girafes, léopards, etc..) sont connus de Descartes dès le 17^èmesiècle.

Diagrammes de Voronoï sur le pelage d’un Léopard

Nous essaierons tout au long du présent article, de vulgariser des notions relatives au transport optimal, par des applications concrètes dont certaines en finance quantitative.

Nous commencerons par citer le parcours de grands mathématiciens qui ont, à travers les siècles, confirmé le caractère central et pluridisciplinaire de ce très vieux problème.

[1]Dans la littérature, les diagrammes de Voronoï sont des objets traités par la géométrie algébrique. Cependant ils sont très liés à la notion de transport optimal.

Quelques grands noms du transport Optimal

Monge

Gaspard Monge – [1746 [Beaune] – 28 juillet 1818 [Paris]-  est reconnu, entre autres initiatives (création de l’école polytechnique, voyage en Egypte sous Napoléon…), pour son apport conséquent à la géométrie différentielle, la combinatoire, le calcul des variations mais aussi la géométrie descriptive.

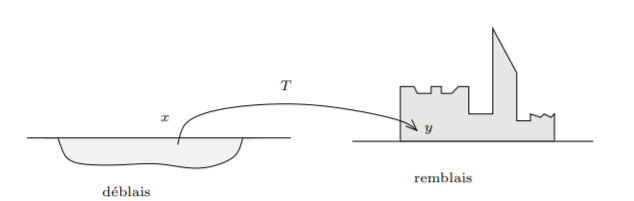
En 1781, il publie un article sur la théorie des déblais et des remblais qui s’articule sur la résolution de la problématique suivante : comment déplacer un tas de sable en minimisant le coût du transport, c’est-à-dire le travail à fournir.

 

La notoriété de ce mémoire sera confortée notamment lorsque l’académie des sciences, en 1884, propose comme sujet de concours pour le prix Bordin, de reprendre cette théorie concernant le transport optimal et de résoudre les cas particuliers associés.

Ci-dessous une illustration du problème de Monge[1].

Kantorovitch[2]

 

 

Leonid Kantorovitch – [19 Janvier 1912 [Saint-Pétersbourg] – 7Avril 1986 [Moscou]-  est un mathématicien et économiste soviétique (calcul scientifique, optimisation linéaire, …). Prix Nobel d’économie, il est reconnu pour l’importance de ses travaux dans le domaine de l’économie mathématique. Il a par ailleurs développé la théorie du transport optimale initiée par Monge.

En outre, il s’est intéressé à d’autres types de problèmes comme la bombe atomique ou l’évacuation de Leningrad prise à l’assaut par les Allemands.

Les travaux de Kantorovitch furent censurés par l’Etat Soviétique. Quelques années après son décès, la communauté scientifique se rend compte que les théories du transport optimal développées par Kantorovitch révolutionnaient les mathématiques modernes par leurs larges spectres d’applications.

Les contemporains

 

En France, la théorie du transport optimal a connu un regain d’intérêt fin des années 80 avec les travaux de Y. Brenier qui s’inscrivent dans la continuité de ceux de Monge & Kantorovitch. Notamment, Brenier montre un résultat fondamental prouvant l’existence et l’unicité d’un chemin de transport optimal qui correspond à un gradient de fonction convexe. En particulier, la R&D de MPG-Partners utilise ce résultat de manière intensive, comme décrit dans la section « applications » de cet article. Cédric Villani, médaille Fields 2010, est quant à lui connu pour l’application de cette théorie dans les diffusions des gaz (Boltzmann) ainsi qu’à la physique des plasmas.

 

Exemples concrets

Dans un problème de transport optimal, le premier concept est la fonction de coût de transport, choisie selon le cas que l’on traite, la contrainte étant que cette fonction soit convexe. Nous définissons également la notion de plan de transfert, qui correspond à déplacer un objet. On peut mesurer le coût d’un plan de transfert par une fonction que nous dénommons « fonction de coût ». Un problème de transport optimal revient alors à trouver le plan de transfert qui minimise le coût de transport. Illustrons le propos :

 

Déplacement d’objets

Par exemple, considérons deux objets A et B placés l’un à côté de l’autre.  On souhaite tout simplement les déplacer de l’état initial dans deux cases, comme le montre le schéma ci-dessous.

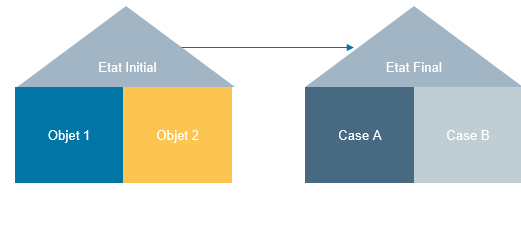Pour ce problème de transport, il y a deux plans de transfert possibles : on peut, soit déplacer l’Objet 1 dans la case A, et l’Objet 2 dans la case B, soit l’inverse.

On peut se convaincre que, si le coût de transport est égal à la distance, alors les deux plans de transfert sont équivalents (le coût de transport est le même). Cependant, si le coût de transport est le carré de la distance, alors il vaut mieux privilégier de petits déplacements (l’Objet 1 dans la case A, et l’Objet 2 dans la case B).

Problématiques discrètes : désert et oasis, union soviétique et google map

Imaginons N personnes dans le désert et N oasis, une oasis ne pouvant abreuver qu’une seule personne. On cherche alors à minimiser l’effort global à fournir (coût de transport) de manière que chaque personne trouve son oasis.

Dans le problème de l’oasis, le coût de transport global est naturellement la somme des distances à parcourir de chaque personne vers son oasis, qui détermine l’effort à fournir.  Par exemple pour N=4, voici un plan de transfert possible :

 

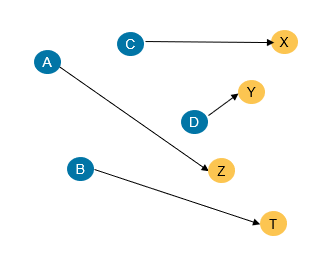
Dans ce diagramme, les boules en bleu peuvent représentent l’état initial des personnes. Les boules jaunes représentent les quatre états finaux, les oasis.  Cependant, il existe d’autres interprétations possibles :

• Si les boules bleues représentent des usines soviétiques, les boules jaunes des divisions de l’armée rouge, et la distance exprimée étant celle donnée par l’état des routes de Sibérie au front de l’est à l’automne 1941 pendant l’opération Barbarossa, il s’agit du problème posé par Staline à Kantorovitch.
• Si les boules bleues représentent des restaurants, représentées sous forme de points, les coordonnées étant données par la distance à l’utilisateur en abscisse, et de la notation culinaire en ordonnée. Les boules jaunes servent de podium, élaboré à l’avance comme référence par les utilisateurs. Alors ce problème de transport permet de faire un choix consensuel dans un groupe dans un contexte de choix multiples, car il permet d’ordonner sans équivoque.

Remarquons que dans ce type de problème, le nombre de déplacement possibles ou plans de transfert est le nombre de permutations possibles entre les deux groupes de boules, qui est N factorielle (N*(N-1) *…*2*1).  Cependant, pour résoudre ce type de problème, la complexité algorithmique (le nombre d’opérations à faire) est bien inférieure, et est de l’ordre de  , N étant le nombre d’états (boules bleues)[3].

 

Transport optimal, problématiques continues

 

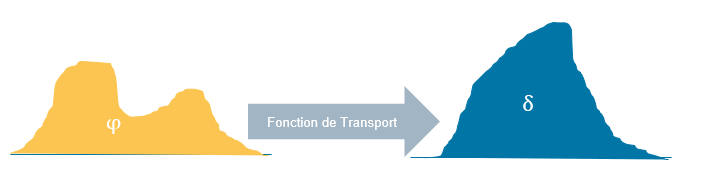
Imaginons un tas de sable (en jaune), que l’on cherche à déplacer de manière à faire une forme de même masse (en bleu). Ce problème, qui est l’objet du mémoire de Gaspard Monge, peut se décrire comme la limite d’un des problèmes discrets présentés plus haut, lorsque le nombre d’états initiaux et finaux deviennent très grands (le nombre N). Dans ce cas, la complexité du problème () semble prohibitive pour espérer le résoudre numériquement.

Cependant, ces problèmes de transport optimaux continus peuvent se traiter d’une manière plus efficace : notamment, le théorème de Yann Brenier cité plus haut affirme l’existence d’un schéma de transfert « optimal », pouvant déplacer ce tas de sable à moindre coût. D’autre part, ce chemin est décrit par l’équation de Monge-Ampère.

Une conséquence notable de ce plan de transfert optimal est que deux grains de sable ayant des points de départ différents seront déplacés selon des chemins (géodésiques) qui ne se croiseront pas.
  

Dualité de Kantorovitch

Dans ce paragraphe, nous expliquons les outils développés par Kantorovitch pour résoudre son problème de transfert décrit plus haut.

Rappelons que ce dernier devait organiser le convoi des productions des usines vers les troupes situées au front de l’est. La production des usines, et la consommation des armées, sont représentées par des mesures positives, les quantités totales étant en adéquation (on suppose que la production sera consommée en son intégralité). Le souci de Kantorovitch est de minimiser le coût dépensé en transport, connaissant précisément les « marginales » du même transport, i.e. la production et la consommation. Nous sommes donc en présence d’un problème de Monge-Kantorovich.

L’idée de Kantorovitch est de sous-traiter le problème de transport, en payant un prix à l’embarquement de la production, et au débarquement, les prix variant bien sûr du lieu d’embarquement et de débarquement. Kantorovitch y met une contrainte : que le prix d’embarquement et de débarquement de chaque marchandise reste toujours inférieur au coût de transport de la marchandise. Cependant, le problème est maintenant sous-traité au convoyeur, qui cherche à maximiser son profit.

Kantorovitch démontre dans son principe de dualité que le profit maximal du convoyeur est égal au coût de transport optimal.

 

Application à la finance

 

On dénombre, pour la théorie du transport, un large spectre d’applications. Une poignée de Mathématiciens du laboratoire CMAP de l’Ecole Polytechnique se sont intéressés[4] aux applications à la finance quantitative qui sont encore aujourd’hui assez peu nombreuses. Ainsi, des résultats en calibrations des modèles hybrides ont pu être démontrés.

 

Transport optimal, et valorisation de produits financiers

 

La théorie du « Transport optimal martingale » utilise les fondamentaux de la théorie initiée par G.Monge  dans les mathématiques financières, et permet par exemple de déterminer des limites de non arbitrage pour des options quelconques.

Par exemple considérons un produit financier très peu liquide, dépendant de sous-jacents (actions / taux / etc..), que nous devions valoriser pour des raisons comptables. Supposons par ailleurs que nous disposons d’un ensemble de prix de marché sur ce sous-jacent, par exemple des prix de produits financiers très liquides (principalement des options, swaptions, etc..).

Le premier problème auquel on fait face est de trouver une variable aléatoire modélisant les sous-jacents et respectant les prix de marché. Ce type de problème est usuellement appelé le problème de la calibration. Or il existe une infinité de processus possibles respectant ces contraintes.

Dans ce contexte, il existe non pas un prix, mais tout un intervalle de prix possibles pour valoriser ce produit. A l’inverse, si ce produit est proposé à un prix hors de cet intervalle, alors il existe une opportunité d’arbitrage, i.e. une stratégie qui permet de gagner en numéraire sans prendre de risques.

 

Dualité de Kantorovitch et sur-couverture de produits financiers

 

Le principe de dualité de Kantorovitch a été appliqué par P.H. Labordère en finance quantitative, pour déterminer des couvertures dynamiques de produits dit exotiques type Look-Back, qui sont des produits dont le payoff dépend de la performance entre deux temps  d’un sous-jacent (action / taux / etc…). On suppose que l’on connaît exactement la distribution du sous-jacent aux deux temps en  et  . On appelle ces deux distributions des « marginales ».

Le problème est de déterminer une stratégie de couverture permettant d’annuler le risque porté par ce type de produits, sachant que l’institution dépositaire peut acheter ou vendre des options sur le sous-jacent.

Le premier problème est similaire à la notion de calibration évoquée dans le paragraphe plus haut : connaissant la distribution d’un sous-jacent aux deux temps , il existe une infinité de processus décrivant ce sous-jacent entre ces deux temps. Il existe donc un intervalle de prix possibles pour ce produit.

D’autre part, si l’on se donne une dynamique du sous-jacent sur tous les temps , cela détermine le prix de notre produit. Dans le formalisme du transport optimal, déterminer le sous-jacent revient à déterminer la fonction de coût de transport mais également un plan de transfert entre les marginales en et  . Dans ce contexte, le principe de dualité de Kantorovitch s’applique : on peut déterminer une couverture au temps et  , correspondant au coût optimal du transport, qui est le prix de notre produit après avoir déterminé le sous-jacent.

Comme on l’a dit plus haut, il existe une infinité de dynamiques possibles pour le sous-jacent entre les temps et . Il existe donc également une infinité de couvertures possibles. La « sur-couverture » (Superhedging) correspond à l’enveloppe de ces couvertures, et permet de ne subir aucun risque quelque soit le chemin de transport, chaque chemin correspondant à un choix possible déterminant la dynamique du sous-jacent de notre produit entre les deux temps et  .

 

CoDeFi : un framework de calcul de risques financiers basé sur le transport optimal

 

Dans le cadre de l’activité de recherche et développement de la société MPG Partners, nous avons développé un outil de mesure des risques, que nous appelons CoDeFi, qui utilise extensivement certains résultats du transport optimal. Nous exposons par la suite quelques résultats de recherche.

 

CoDefi : carte de transport

 

Carte de transport : Rappelons une conséquence du résultat de Y.  Brenier : pour deux mesures de probabilité, il existe une unique carte transportant une des mesures dans l’autre et qui s’écrit sous la forme d’un gradient d’une fonction convexe. Cette carte correspond au transport optimal d’une mesure dans l’autre.

Nous utilisons très extensivement ce résultat : en mathématiques financières, les sous-jacents des produits financiers sont vus comme des processus stochastiques. Ils possèdent donc une densité de probabilité, qui est une mesure des évènements futurs. Cependant il est très coûteux en termes de temps de calculs de simuler tous les évènements possibles. Pour cela, on se ramène à l’espace d’évènements contenus dans le cube unité, en déterminant et calculant explicitement la carte transportant la mesure uniforme du cube vers la mesure de densité du sous-jacent que nous étudions. Cela permet notamment de travailler sur des espaces d’évènements équiprobables.

 

CoDefi : approximation numérique

 

Un problème très courant en analyse numérique est le calcul de l’intégrale d’une fonction. Ce problème est à la base de la célébrée méthode de Monte-Carlo, mais apparaît dans de très nombreuses autres branches des mathématiques, notamment les équations aux dérivées partielles. Rappelons que l’erreur commise par la méthode de Monte-Carlo s’écrit de la manière suivante : pour toutes fonctions , on a

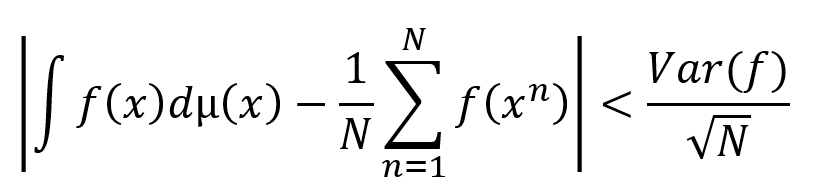
Où  est la variance, et  sont des échantillons i.i.d. (indépendants et identiquement distribués) de la variable aléatoire de densité µ. On dit donc que la méthode converge en  . La question se pose : existe-t-il des échantillons pour lesquels nous pouvons espérer une convergence plus rapide ? La réponse est oui, et nous savons les calculer numériquement. En particulier, pour les fonctions classiquement utilisées en Finance (des sommes de calls et de puts), nous exhibons des taux de convergence en  , c’est-à-dire quatre ordres de magnitude plus efficaces. Pour donner un exemple, calculer une intégrale en utilisant 100 de ces points est aussi efficace que les méthodes de Monte-Carlo classiques utilisant 100 millions de points. Ce résultat permet de réduire drastiquement les temps de calcul dans nos algorithmes. Ce problème est un problème s’apparentant au transport optimal : il s’agit de trouver une distribution discrète approchant au mieux la densité de probabilité continue d’une variable aléatoire.

 

 

Transport optimal : conclusions et perspectives

 

Comme nous avons pu le détailler dans les paragraphes précédents, la théorie du transport, lors des dernières décennies, s’est étendu aux mathématiques financières, cependant les applications restent toutefois limitées par rapport à d’autres domaines (traitement de l’image, mathématiques fondamentales etc).

Le transport optimal, s’applique en outre aux problématiques d’optimisation et de programmation linéaires dont les applications revêtent aujourd’hui une importance accrue.

Citons une autre application concrète : la théorie de l’économie urbaine, dans laquelle et grâce au transport optimal, il est possible de relier la structure de villes et de métropoles et la compétitivité des entreprises s’y trouvant. Ainsi un équilibre s’établit entre la densité des habitants dans une zone donnée et la densité des emplois sur cette même zone.

In fine, les applications très variées de ce très vieux problème, suscitent de plus en plus l’intérêt de nombreux chercheurs, les usages en mathématiques financières sont récents et on ne peut que leur prédire un essor important au cours des prochaines années.

 

[1]Optimal transport Old and New. Cédric Villani

[2]Portrait de Kantorovitch par le peintre Vodkine en 1938.

[3]Cf par exemple Yann Brenier – https://interstices.info

[4] http://www.cmap.polytechnique.fr/~euroschoolmathfi12/lect1Part1.pdf