Amélioration des taux de convergence pour les méthodes type Monte-Carlo et EDP (Equations aux Dérivées Partielles)

Jean-Marc Mercier, Senior Research Advisor, MPG Partners

 

Introduction

Dans ce post, nous présentons succinctement des résultats numériques qui nous semblent intéressants à la fois pour les simulations numériques utilisant les méthodes de Monte-Carloet aussi pour les méthodes de type EDP (Equations aux Dérivées Partielles).

Ces résultats sont basés sur une nouvelle méthode numériquequi permet de calculer explicitement des échantillons Monte-Carlo pour une très large classe de processus stochastiques : nous pouvons produire ces échantillons pour tout processus stochastique défini par une EDS(Equation aux Dérivés Stochastiques) en très hautes dimensions, c’est à dire avec grand nombre de facteurs de risques (D >> 4).Nous L’avons testé pour l’instant jusqu’à 64 dimensions.

Nous illustrons les propriétés qualitatives de ces échantillons ainsi que les performancesde cette méthodelorsqu’elle est utilisée conjointement par un moteur EDP. L’illustration choisie est une application de la mathématique financière, correspondant à un calcul de risque réglementaire (VAR – Value At Risk- et EE –ExpectedExposure) d’un portefeuille d’AutoCalls.

Propriétés Qualitatives des échantillons

Les échantillons calculés ont la particularité d’être très bien distribués, rappelant la distribution qui serait obtenue par des méthodes de type quantification optimale. Notamment, pour le calcul d’intégrale de fonctions (espérance), nous mesurons sur certaines classes de fonctions des taux de convergence qui sont meilleurs que les méthodes de Monte-Carlo classiquement utilisées, et ce d’un facteur d’échelle.

Pour illustrer cette répartition, nous présentons dans les figures suivantes trois échantillons de N=256 points provenant de trois méthodes d’échantillonnage. Le processus stochastique étudié est un processus Log-Normal bivarié, corrélé négativement (-0.5), dont chaque composante univariée possède une volatilité de 10%. Le processus est étudié au temps t = 1.

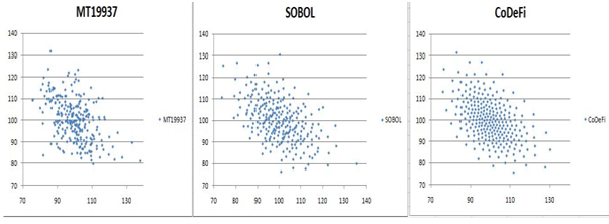
La première figure à gauche (libellée MT19937) représente la génération de 256 échantillons calculés par un générateur pseudo-aléatoire type Mersenne Twister, un standard dans l’industrie. Ce générateur possède un taux de convergence bien connu :

où la constante apparaissant à droite est la variance de P, considérée comme une variable aléatoire au temps 1.

La deuxième figure (libellée Sobol) au centre représente la génération de 256 échantillons calculés par un générateur de Sobol, qui est générateur  quasi-aléatoire utilisé industriellement. Ce générateur, motivé par une meilleure répartition des points d’échantillonnage, possède un taux de convergence qui est conjecturé, à notre connaissance:

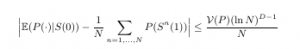
où la constante apparaissant à droite est la variation bornée de la fonction échantillonnée P, N le nombre de points d’échantillonage, et D la dimension. Ces taux de convergence sont meilleurs qu’un générateur pseudo-aléatoire lorsque le nombre d’échantillon N est grand. Cependant, la qualité de l’échantillon se dégrade rapidement lorsque que la dimension du problème augmente.

La troisième figure à droite (libellée CoDeFi) représente la génération de 256 échantillons calculés par cette nouvelle méthode. Numériquement, ces échantillons présentent quelques propriétés intéressantes, outre la régularité de leur distribution qui est frappante. Tout d’abord, leur taux de convergence est toujours au moins aussi bon que les deux autres suites (MT19937 et SOBOL) sur tous les exemples que nous avons étudiés. D’autre part, ces échantillons présentent des taux de convergence du type

Pour une classe de fonctions P, qui sont largement utilisées notamment en Finance, comme les calls et les puts, où la constante qui apparaît à droite mesure une forme de régularité de P et qui, numériquement, sembleindépendante de la dimension D. C’est un résultat surprenant : nous mesurons quatre ordres de magnitude au dessus d’une méthode de Monte-Carlo pour la classe de fonctions. Par exemple, cela signifie qu’un échantillon de 100 points, calcule une espérance avec la même précision que 100 millions d’échantillons utilisant un générateur MT19937, quelques soient le nombre de dimensions. Ce pourrait donc être un gain appréciable en terme de complexité algorithmique. Bien sûr, la contrepartie est que ces suites d’échantillons sont plus difficiles et longues à calculer[1] que des suites type pseudo ou quasi aléatoires.

[1] Pour être précis, l’algorithme qui calcule ces suites possède une complexité algorithmique (le nombre d’opérations faites par l’ordinateur) de l’ordre de D N³

Application aux méthodes type EDP, illustration par un calcul de risque réglementaire

Le résultat du test que nous présentons ici ont été réalisé avec CoDeFi, un framework permettant la valorisation de produits dérivés complexes, de portefeuilles, ainsi que le calcul de leurs indicateurs de risque, ou d’évaluation de stratégies complexes comme les limites de risques par exemple.

CoDeFi est basé sur une technique hybride EDP/Monte-Carlo. L’idée phare de ce solveur EDP hybride est d’utiliser des trajectoires Monte-Carlo pour produire des grilles de calcul utilisée par le solveur EDP. Notamment, nous pouvons utiliser comme grille EDP les trajectoires produites par un générateur MT19937, ou encore Sobol, maisCoDeFipropose également de calculer ses propres trajectoires.Notamment, la figure précédente correspond à trois grilles de calcul EDP utilisables par CoDeFi au temps 1, en dimension 2. Dans ce test, nous illustrons le comportement obtenu en utilisant les grilles de calcul produites par CoDeFi, i.e. la troisième figure en dimension deux (label CoDeFi).

L’objet de ce test est de qualifier quantitativement les performances de ces grilles pour le moteur EDP de CoDeFi. Ce test est défini tout d’abord par la donnée d’un processus stochastique et d’une fonction définie sur ce processus :

• Le processus est un Log-normal univarié (D=1), volatilité 10%.
• La fonction est celle d’un instrument financier, qui est appelé un AutoCall. Ses caractéristiques sont : maturité cinq ans, date d’observation de maturité annuelle (1,2,3,4,5 ans). La barrière AutoCall est de 100%, la barrière de coupon est de 80 %.

Puis, le test présenté ne dépend que de deux paramètres : D la dimension, N le nombre de points. Pour une dimension D donnée, on définit d’abord un processus D dimensionnel de la manière suivante :

• Chaque processus marginal est défini comme une copie du processus univarié ci-dessus.
• Une corrélation constante est imposée entre chaque marginale.

Puis on définit un portefeuille d’AutoCall de la manière suivante :

• On définit tous les Autocallunivariés, comme une copie de l’Autocall défini ci-dessus, en changeant le sous-jacents. Il y a donc D Autocallunivariés.
• On définit tous les Autocallbivariés (AutoCallworst-of), comme une copie de l’Autocall défini ci-dessus, en prenant toutes les combinaisons parmi deux : il y a donc D(D-1)/2 Autocallbi-variés.
• Etc…jusqu’à définir le dernier AutocallD-varié, qui est un AutoCallWorst-of écrit sur D sous jacent.

Ce portefeuille,ainsidéfini,contient exactement 2 à la puissance D Autocalls.Cependant, dans le contexte de ce test, seuls D Autocallssont réellement différents : nommément chaque AutoCalld-variés, avec d entre 1 et D. Nous pouvons notamment estimer numériquement les prix et les sensibilités de chacun de ces AutoCall par une méthode de Monte-Carlo classique utilisant un grand nombre de trajectoires.

Enfin, nous générons les grilles de calcul et résolvons par EDP l’équation de Kolmogorov Backward (appelée aussi équation de Black and Scholes) en utilisant une grille de N échantillon.

Par exemple la figure suivante illustre le cas D=10, N=512 : nous présentons les 10 prix calculés par Monte-Carlo en abscisse, et en ordonnée les prix calculé par EDP par CoDeFi sur les 2^10 = 1024 Autocalls.

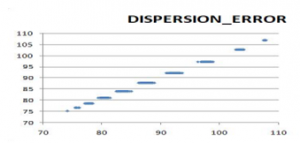
Pour ce test, nous mesurons deux choses :

• L’erreur globale sur l’ensemble du portefeuille de 1024 AutoCall est de 0,2 % sur le prix, ce qui correspond à un facteur de convergence 1/N.
• Le temps consommé par l’algorithme pour calculer les prix de ces 1024 AutoCalls, ainsi que leur 1024*10 sensibilités de premier ordre (delta), ainsi que les 1024*45 sensibilités du second ordre (gammas), ainsi que la VAR (Value At Risk de marché) de ce portefeuille, ainsi que l’EE (expectedexposure) de ce portefeuille, en utilisant un cœur d’un processeur Intel I7, est de 20 secondes. On note également que les temps d’exécution de ce test, pour les dimensions 11 (2048 AutoCalls), 12 (4096 Autocalls), 13 (8192 AutoCalls), restent inférieurs à la minute, pour des taux de convergence qui restent stables.

 

 

Conclusions

Nous avons choisi d’illustrer les gains de performances obtenues par ces suites dans un cas qui est peu avantageux[1]. Cependant, même dans ce cas, la méthode proposée montre un gain très appréciable en terme de performance pour les calculs de type risques réglementaires[2].

[1]en effet, la fonction correspondante à un AutoCall est une fonction à variation bornée, une classe de fonction pour laquelle nous savons que les taux de convergence d’une méthode d’échantillonnages ne peuvent dépasser 1/N.

[2] Notamment, nous ne connaissons aucune autre méthode numérique capable de réaliser ce test, avec ce niveau de précision (0,2% sur les prix, sur la VAR et l’EPE), et les moyens informatiques dont nous disposons.